Building a Text Editor in Haskell, Part 1
27 Mar 2024
I am building a little text editor in Haskell.1 Why would I do such a thing? Because I’m in a class and this fulfills the requirement, and building a text editor is the kind of thing that I’ve always wanted to take a crack at.
This is part 1, and I will describe how to build a rope data structure in Haskell. A rope is a bunch of strings (literally, and in the CS sense) and is optimized for cheap edits. You can see my implementation on Codeberg.
Why ropes? #
This has probably been discussed ad nauseam, but I’ll throw a brief justification for using a rope here to save you a click/search. Warning: this is not going to be in-depth or anything, so if you’re not persuaded that e.g. ropes are a good idea, it’s probably because I am trying to be brief here.
Here’s the problem: when you’re working in a text editor, you usually are doing edits somewhere in the middle of the file. If you were to store a buffer of \(n\) characters in an array, inserting a character at position \(i\) would mean that you have to move all \(n - i\) characters after that point over one slot in memory—which gets extremely expensive for even moderately sized files. This leaves out the complexity of having to re-allocate the array periodically as it grows. Yuck!
Ropes, on the other hand, store bits of text in a balanced binary tree. Inserting some text never mutates existing nodes; instead, new nodes from the modified leaf up to the root (so, roughly \(\log(n)\) nodes) need to be allocated on insertion.
This comes with two benefits: first, insertion and deletion scale extremely well. Second, since the structure is immutable, you could store the last \(k\) copies of the string to implement an “undo” feature in your editor. Moreover, all the chunks that didn’t get changed don’t take up any extra space, since the data structure enjoys nice structural sharing.
“But what about all those nodes you need to allocate?” you might well ask. Modern garbage collectors are so good these days you won’t even notice. As soon as you’re working with a new copy of the string, or as soon as a copy of the string you’ve been holding onto in your undo buffer gets bumped out, the garbage collector is sure to swiftly reclaim any nodes no longer in use.
Benchmarks #
I implemented a rope and ran some benchmarks, comparing it with a naïve string insertion algorithm. Note: reproducing these in other languages will differ based on how your language implements strings. I’m using Haskell, which represents strings as linked lists of characters. This has some trade-offs:
- Indexing into the \(n\) -th element takes \(O(n)\) time, which isn’t great.
- However, joining a string onto the head of another only requires that you walk the first string to its end; you do not have to walk the entire length of the end string.
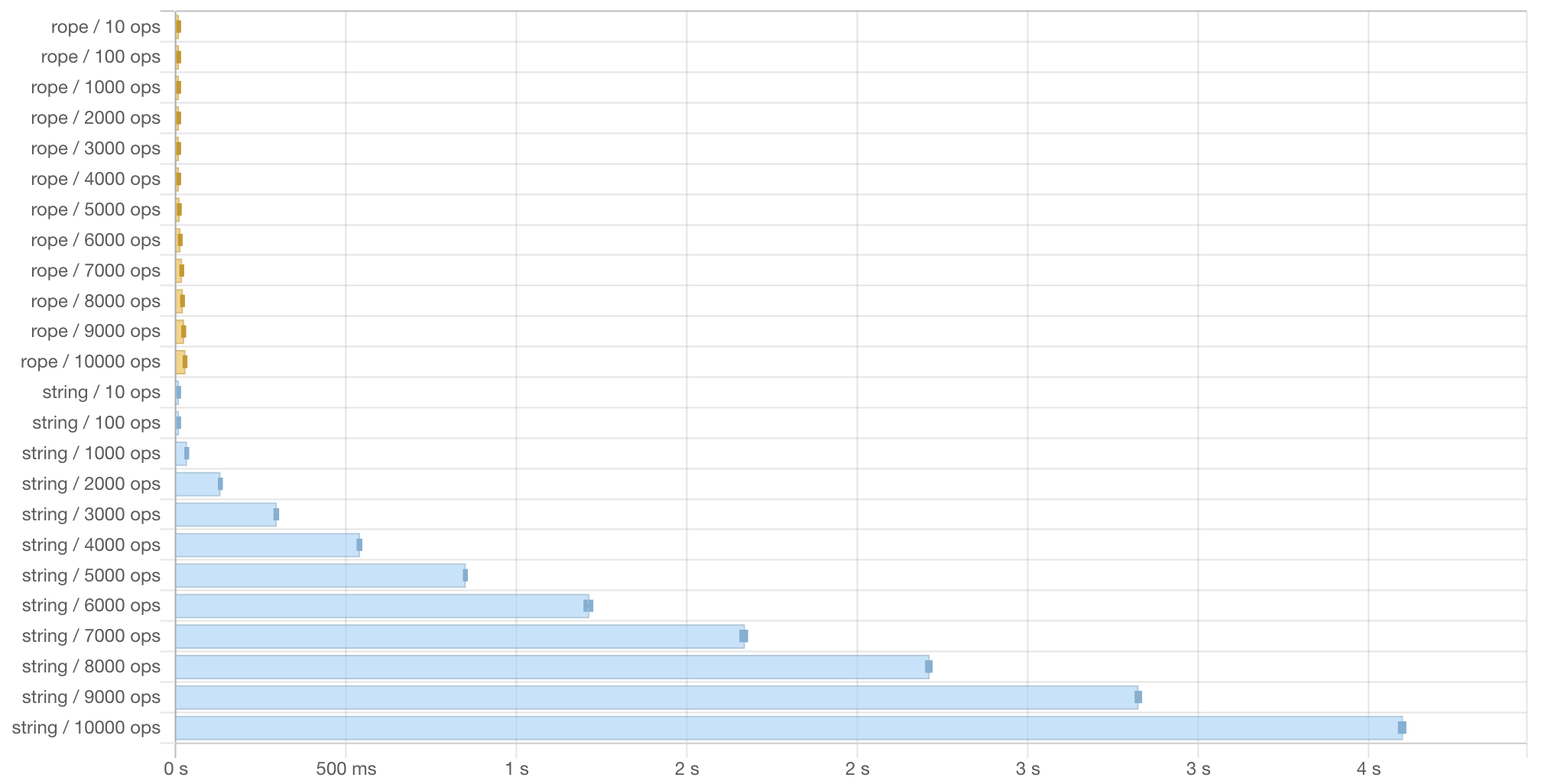
Figure 1: Benchmark report comparing a series of random edits applied to a rope vs. a string. The rope shows minimal difference in time taken to perform 10 random edits (4.03 μs = 0.004 ms) to 10,000 edits (28.1 ms). In contrast, the naïve string implementation jumps from 2.56 μs = 0.002 ms for 10 edits all the way to 3.6 s = 3600 ms for 10,000 edits.
I tried running the benchmarks for 100,000 random edits, and the last benchmark never finished even though I let it sit for over an hour. Arrays of characters are not sustainable for editors.
Building a rope #
The original rope paper [1] and the Wikipedia article on ropes both do a fine job of explaining the data structure. I’ll just outline some gotchas here.
The data structure #
Here’s my definition of a rope:
data Rope
= Concat Int Int Rope Rope -- Concat length height left right
| Leaf Int String -- Leaf length content
deriving (Show, Eq)
A rope is either a Leaf node or a Concatenation of two rope nodes. The Leaf variant contains two fields: a regular ol’ string as well as how long the string is.2 The Concat variant holds left and right subtrees, the total length of its subtrees, and how high up in the tree it is. (This is important for balancing later on.)
The string gets broken up between the leaves and the concat nodes hold everything together.
Why do Concat nodes need to hold their length? This is to speed up searching through the tree: since every node knows how long the string underneath it is, we don’t need to go all the way down to the leaves to figure out where in the string we should jump if we’re looking for, say, the 1000th character. This keeps accesses
\(O(\log(n))\)
which is pretty fast.
Balancing algorithm #
The balancing algorithm is the trickiest part of implementing a rope, and it’s a bit of a shame that the paper doesn’t have better examples. I did use the paper as a reference to implement the algorithm, so it was clear enough, but more examples are always good!
Alternatives to ropes #
The Rhombus language uses an RRB tree [2] for it’s primary list data structure. RRB trees would probably work pretty well for text editing. You can see the Rhombus implementation on GitHub.
References #
-
I call it “ysue”, for You Should be Using Emacs. It actually works! I used it to edit its own source code! Get it here: https://codeberg.org/ashton314/ysue ↩︎
-
Haskell strings are linked lists. This is nice for all sorts of functional operations, but it means that they don’t track how long they are. (As far as I know.) If you use a language that can get the length of the string in \(O(1)\) time, you might not need this. ↩︎